モードドライバー第2回(おまけ)
前回はMatlab/ Python連携を簡単なモデル作って試してみました。そのpythonファイルは3元方程式のをサポートベクタ回帰するものでした。わかりやすくするために簡単な放物線を取り扱ってみました。
モードドライバも3元(速度、加速度、アクセル開度)を扱うものなのでちょこっと変更すれば使えそうなのが想像できます。というか、引数をシミュレーション結果を与えるだけなのでちょっと試してみました。
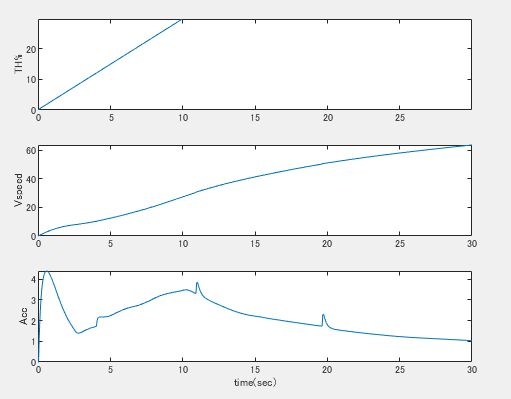
こんな感じのパターンシミュレーション開始から10秒でランプ状にアクセルを踏み10秒後30%開度のところで30秒迄ホールドした場合の挙動です。真ん中の車速はほぼ直線的に車速が上昇しているのがわかります。しかし、下の加速度を見てみるとアクセルを踏み始めた初期に最も大きな加速度が得られ一旦降下したのちに緩やかな山状に加速度が変化しています。途中パルス状の加速度が発生している部分は変速ショックです。1→2速、2→3速、3→4速と変化するたびに発生しています。
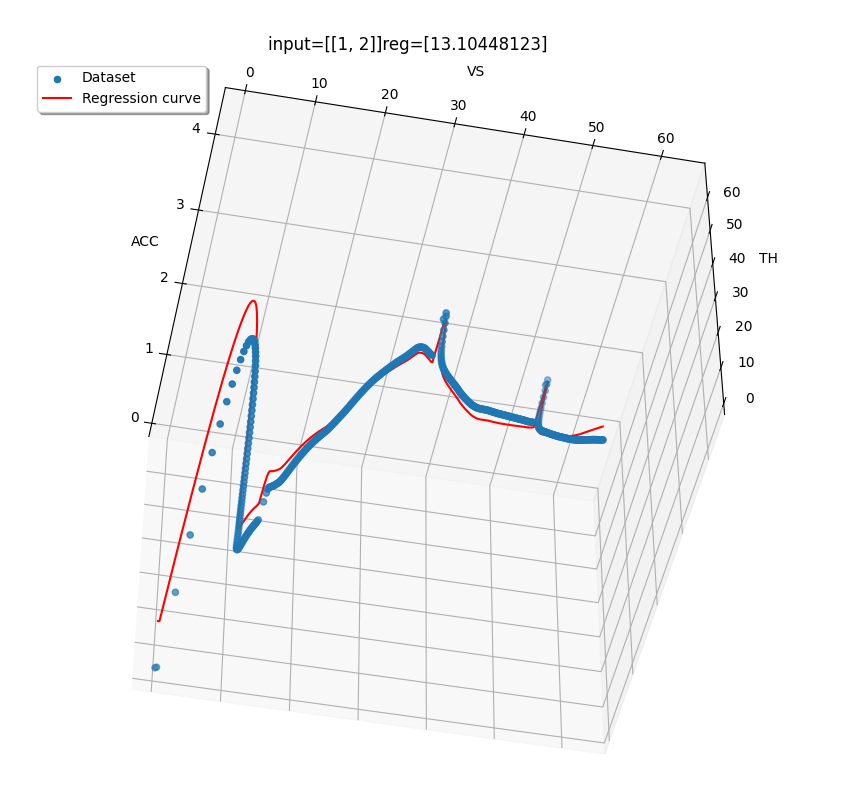
この3データをxyz2.pyに与えた結果がこのグラフです。1例をサポートベクタ回帰しただけですが形状としては青点の学習データに対し赤線の回帰曲線も形状は結構似た形になっています。
import numpy as np
from sklearn import svm
import matplotlib.pyplot as plt
# データ
a = 5.0
b = 0.5
x = np.array(x) #MATLAB引数
y = np.array(y) #MATLAB引数
xy=np.vstack([x,y]) #SVM用データ
noise = np.random.normal(loc=0, scale=0.5, size=len(x))
#z = a*x**2+ b*y +noise
z=np.array(y)
z=z.tolist() #MATLABへの戻り値
# サポートベクターマシン
# 学習
model = svm.SVR(C=1.0, kernel='poly', degree=2,epsilon=0.1)
model.fit(xy.T, z)
# 予測
xy_sample = [[1,2]]
y_reg = model.predict(xy_sample)
print(xy_sample,y_reg) #予測結果参考(1点)
y_reg2 = model.predict(xy.T) #予測結果グラフ用
r2 = model.score(xy.T, z) # 決定係数算出
# グラフ(3D)
#fig = plt.figure()
fig, ax = plt.subplots(figsize=(6, 6), subplot_kw={'projection' : '3d'})
#ax=fig.add_subplot(1, 2, 1, projection='3d')
ax.scatter(x,y,z, label='Dataset', lw=1, marker="o")
ax.plot(x,y,y_reg2, label='Regression curve', color='red')
ax.legend(loc=2, shadow=True) # 凡例
ax.set_title('input='+str(xy_sample)+'reg='+str(y_reg)) # タイトル
ax.set_xlabel('ACC')
ax.set_ylabel('VS')
ax.set_zlabel('TH')
plt.show()
plt.close()これを複数パターン実行して精度が高まればなと思います。第3回はシミュレーションモデル(Simulink)をどの様に改修したか書こうと思います。