モードドライバー第4回(その2)
STEP3.Simulinkのオープンループで学習。
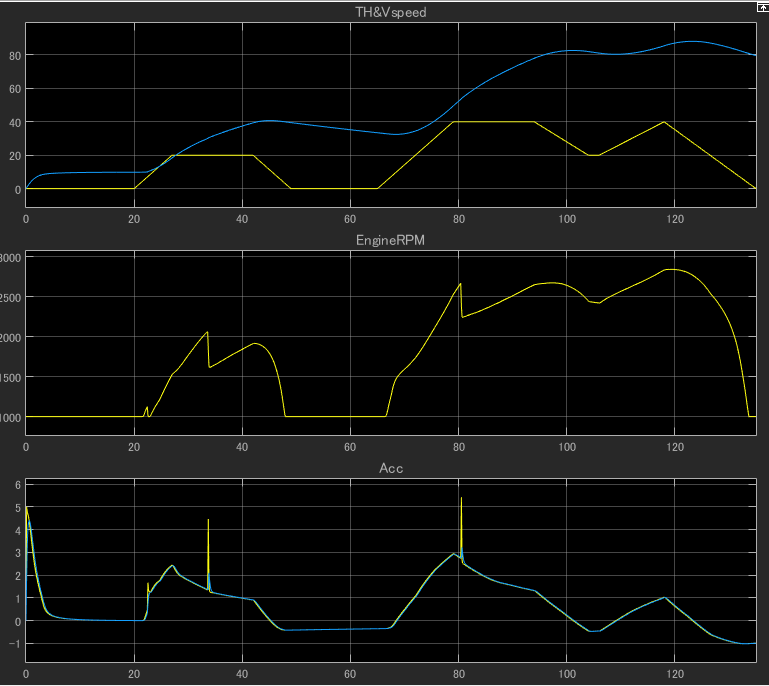
ではオープンループで学習します。こんな感じになりました。一番上の黄色がアクセル開度、青色が車速、中央がエンジン回転数、下の黄色が加速度、青色がそれに適当なローパスフィルタを通したものです。
スタート時アクセル開度が0%にもかかわらず車速が上がっているのがわかります。また車速が上昇しアクセルを話(0%)にしても車速の変化は乏しいことがわかります。そしてこの135秒間の間に車速が80km/hを超えていることがわかります。
この結果を用いてpythonで学習してみます。方法はいくつかありますが、ワークスペースに展開されたスコープデータやmatファイルに保存したデータを一旦Matlabワークスペースに展開して引数としてpythonに与える方法で進めます。
load('learn.mat');
AC=learnsim(6,:);
TH=learnsim(2,:);
VS=learnsim(4,:);
T_AC=learnsim(7,:);
subplot 411
plot(AC)
grid on
subplot 412
plot(TH)
grid on
subplot 413
plot(VS)
grid on
subplot 414
plot(T_AC)
grid onTo Fileブロックにいろんなデータを配列形式でmatファイルに保存することにしました。
learn.matが保存ファイルでlearnsimが変数名で1行目を時間データとした単純な配列データです。こうした理由はラベルなどもなく最もシンプルな形で扱いやすいからです。
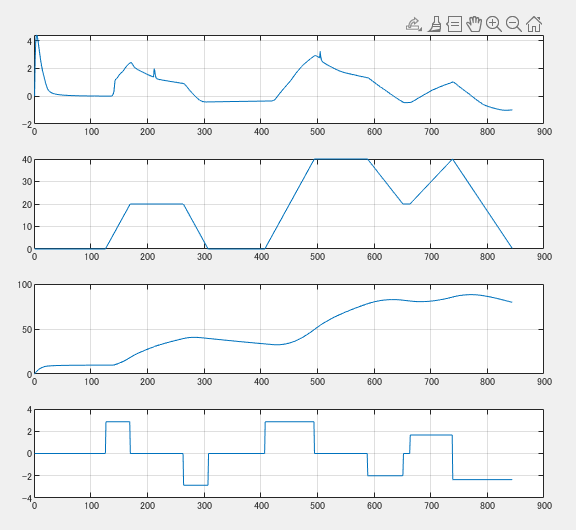
学習に必要なものは実アクセル開度、実速度、実加速度で、回帰に必要なものは目標速度、目標加速度の合計5変数が必要となりますがこのうち実アクセル開度と目標速度は兼用したためpythonの学習&回帰プログラムに必要な引数は4つとなります。
補足ですが目標加速度についてはエクセルで差分をとって作るやり方もありですがここではシミュレーション実行時、車速パターンの後に微分ブロックをつけてSimulink上で作ってみました。
ではpythonにこれらのワークスペース変数を引き渡して回帰パターンを取得してみます。本来ならMatlabワークスペースに結果を展開したかったのですが諸事情によりmatファイルに保存することとしました。
pyrunfile("learndayo.py",x=AC,y=VS,z=TH,zx=T_AC)これがmatlabでのコマンドです。そしてpythonの学習&回帰ファイルは下記のとおりです。動作確認用のファイルから拡張して無理やり作ったため見にくいコードになってしまいました。特にルックアップテーブル用は見苦しいですがご勘弁を。
なおpythonではscipyを使うことによりmatファイルのデータを扱うことができるので最下部にその方法でmatファイルを保存することにしました。本当はmatlabワークスペースに展開したかったのですが結構面倒だったので・・・
import numpy as np
from sklearn import svm
import matplotlib.pyplot as plt
#2-Dルックアップ用
aaa = np.arange(-1.5,5,0.5)
bbb = np.arange(0,95,5)
AAA, BBB = np.meshgrid(aaa,bbb)
AABB=np.hstack([AAA.reshape(-1,1),BBB.reshape(-1,1)])
# データ
x = np.array(x) #MATLAB引数(加速度)
y = np.array(y) #MATLAB引数(速度)
z=np.array(z) #MATLAB引数(アクセル開度)
xy=np.vstack([x,y]) #SVM用データ
# サポートベクターマシン
# 学習
model = svm.SVR(C=30.0, kernel='rbf', degree=8,epsilon=0.1)
model.fit(xy.T, z)
# 予測
y_reg2 = model.predict(AABB) #予測結果グラフ用
r2 = model.score(xy.T, z) # 決定係数算出
# グラフ(3D)
fig, ax = plt.subplots(figsize=(6, 6), subplot_kw={'projection' : '3d'})
ax.scatter(x,y,z, label='Dataset', lw=1, marker="o")
ax.scatter(AAA.reshape(-1,1),BBB.reshape(-1,1),y_reg2, label='Regression curve', color='red')
ax.legend(loc=2, shadow=True) # 凡例
ax.set_xlabel('ACC')
ax.set_ylabel('VS')
ax.set_zlabel('TH')
plt.show()
plt.close()
#回帰データ2-Dルックアップ用
zzz=np.array(y_reg2)
AABBZZ=np.hstack([AAA.reshape(-1,1),BBB.reshape(-1,1),zzz.reshape(-1,1)])
AABBZZ=AABBZZ.tolist()
# mat保存
import scipy.io
scipy.io.savemat("learnkaiki.mat", {'name':AABBZZ})
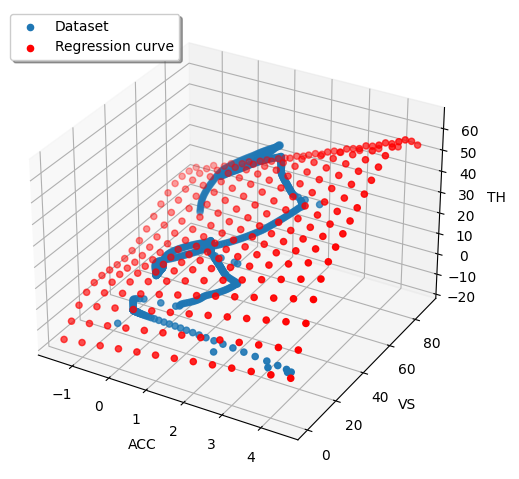
第2回のおまけで学習データの回帰曲線を描いてみましたが、シミュレーションするには目標速度、目標加速度の取りうる値すべて網羅する必要あるので赤点の様な局面が必要となるわけです。
こうしてみると”ある車速である加速度を得るためにはどの程度スロットル開度が必要になるのか?”というものを表現しているのがわかります。これが正しいかどうかはひとまず置いといて次に移ります。
STEP4.回帰曲線の作成(アクセルパターンの作成)。
サポートベクタ回帰はメッシュデータでなく行ベクトルで返してくれるのでそれをリシェイプしてメッシュデータに変更します。その後ドライバモデルのアクセル部に2-Dルックアップテーブルにデータを入れれば完成です。
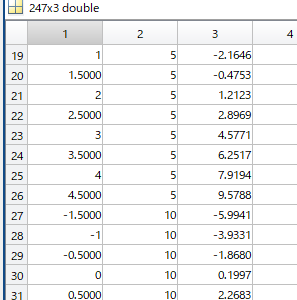
1列目が目標加速度、2列目が目標車速、3列目がアクセル開度
NA=reshape(name(:,1),[13,19])
NB=reshape(name(:,2),[13,19])
NC=reshape(name(:,3),[13,19])
surface(NA,NB,NC)
view(3)
grid onsurfaceは確認のためプロット列ベクトルをリシェイプしてメッシュデータに変換
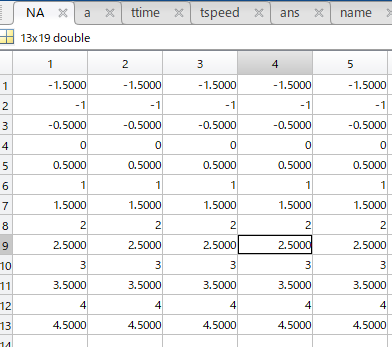
これがメッシュデータ。
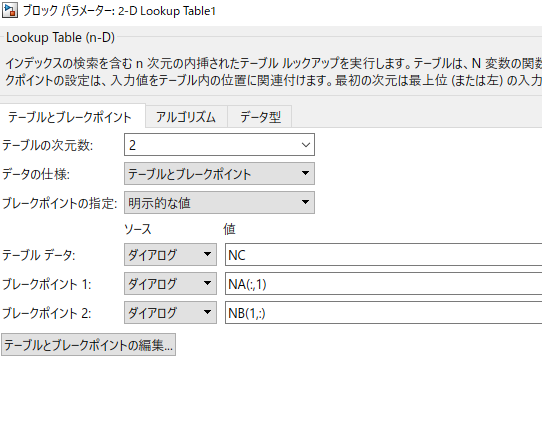
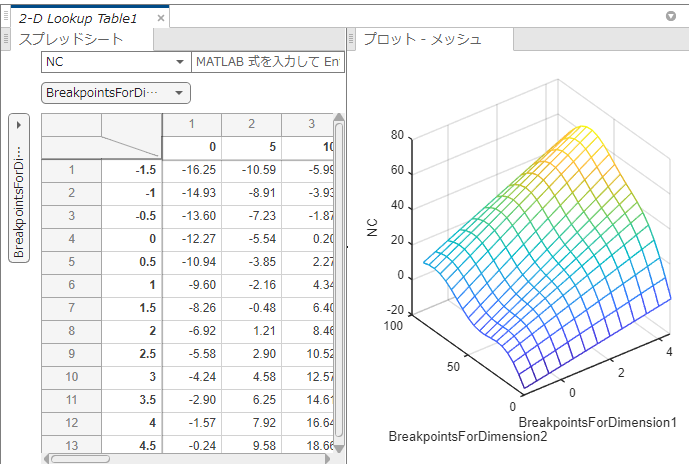
ルックアップテーブルの入出力関係を入れるとマップを表示してくれます。pythonの結果と同じですね。
こうしてSimulinkのデータをpythonに引き渡し学習と回帰を行い再びSimulinkに引き渡すことができました。あとはシミュレーションで確認です。