モードドライバー第2回
今回は車両モデルについて考えてみます。
一から車両モデルを作るのは大変困難なためSimulinkデモの”オートマチック トランスミッション コントローラーのモデル化”というサンプルを使ってみたいと思います。(作成者はThe MathWorks, Inc.)
このモデルは4AT車両で任意の操作量を与えて自動車の挙動を見るもので、実行すると30秒間のシミュレーション結果が得られます。
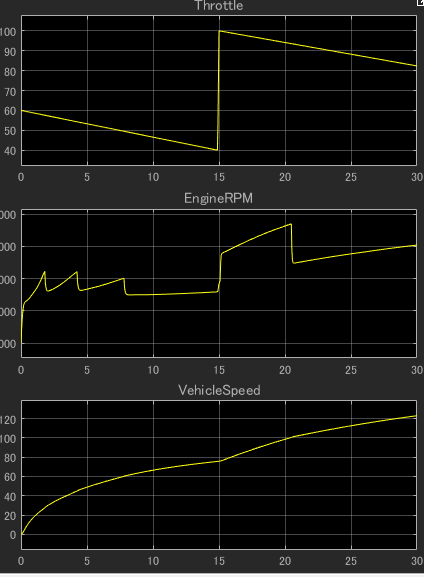
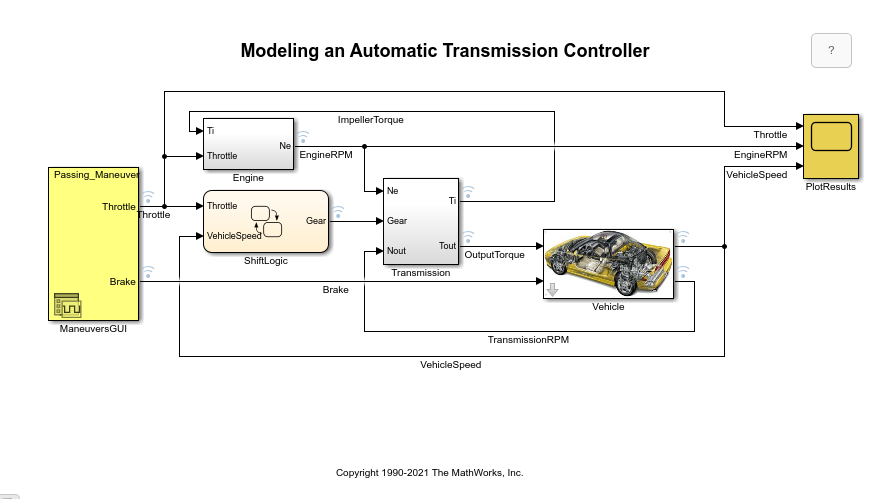
このモデルの左側黄色部分のManeuversGUIがアクセル、ブレーキパターンでして主にこの部分を変更してモデリングします。加速に限定していえばアクセルというのは車速というよりも駆動力を得るために操作するので出力としては加速度が必要となります。
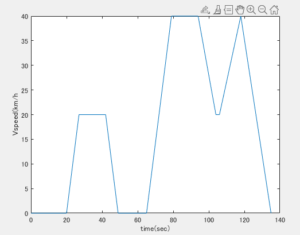
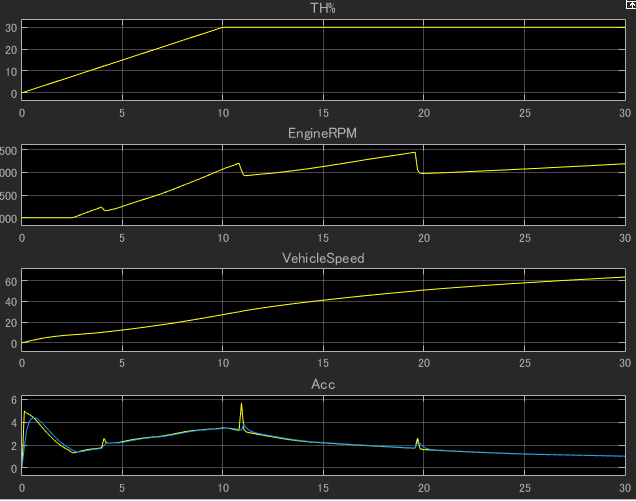
若干モデルを修正してこんな感じでアクセルは10秒間ランプ状で30%まで行ったら保持した場合の挙動です。注目したいのは4秒、11秒、19秒くらいのところで変速しギアが切り替わっているために加速度は大きなショックがでていることがわかります。
機械学習するのに好ましくないであろうと思われるのでローパスフィルタを入れて波形をなました青色の値を使いたいと思います。
STEP1.モードパターンの作成
STEP2.pythonのニューラルネットワークやサポートベクターマシンを記述
STEP3.python⇒Matlab
こんなステップで進めます。
STEP1.モードパターンの作成
前回こんな記述をしました。
- アイドリング状態(20秒) 2.20km/hまで加速する(7秒)・・・
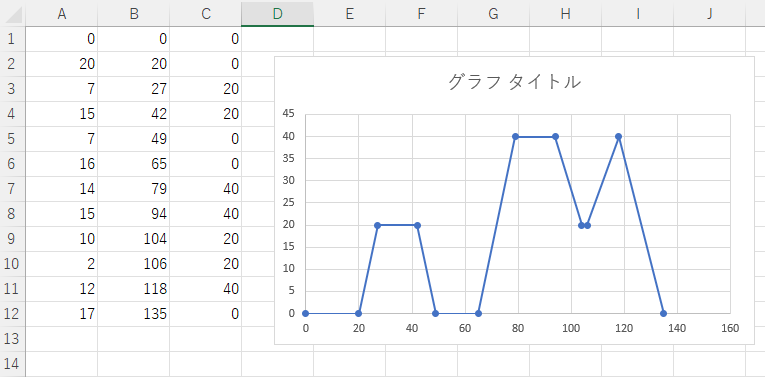
作り方はいろいろありますがEXCEL使ってモードごとの時間を延べ時間に変換、それに対応する車速を入力します。それをMatlabのワークスペースを作って貼り付けすればOKです。それを線形補間してより細かく表現します。
a=0
#変数aを開いてエクセルのデータをコピペする
save "mode10.mat" a
tspeed=interp1(a(:,1),a(:,2),[0:1:135]')'
ttime=[0:1:135]'
scatter(ttime,tspeed)こんな感じです。最終的には恐らく目標車速および目標加速度から所望のアクセル開度を求めるという問題を解くことになると思うので、車速パターンだけでなく加速度(車速変化率)のデータを作る必要がありますがひとまずここまで。
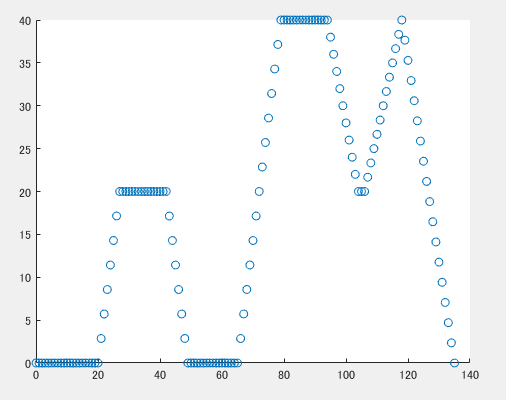
interp1というコマンドでもともと10数点のデータを1秒単位で補間しました。
STEP2.pythonのニューラルネットワークやサポートベクターマシンを記述
車速、加速度、アクセル/ブレーキ開度の関係としてはアクセル/ブレーキによりエンジントルクや車両の減速度に直接影響を及ぼし、それが車速や走行抵抗、変速段などにも影響を受けますが、細かい条件を挙げていたらきりがないので車速、加速度、アクセルの関係を求めるような形にします。
いきなり記述するのでなく、簡単な3元2次式でまとめてみます。
import numpy as np
from sklearn import svm
from matplotlib import pyplot as plt
# データ
a = 5.0
b = 0.5
x = np.arange(-5, 5.0, 0.02)
y = 2*np.arange(-5, 5.0, 0.02)
xy=np.vstack([x,y])
noise = np.random.normal(loc=0, scale=0.5, size=len(x))
z = a*x**2+ b*y +noise
# サポートベクターマシン
# 学習
model = svm.SVR(C=1.0, kernel='rbf', degree=2,epsilon=0.1)
model.fit(xy.T, z)
# 予測
xy_sample = [[1,2]] #検証用
print(xy_sample,y_reg)
y_reg = model.predict(xy_sample) # 予測
y_reg2 = model.predict(xy.T)
r2 = model.score(xy.T, z) # 決定係数算出
print(r2)
# グラフ描画
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.scatter(x,y,z, label='Dataset', lw=1, marker="o")
ax.plot(x,y,y_reg2, label='Regression curve', color='red')
plt.legend()
# グラフを表示する。
plt.show()
plt.close()
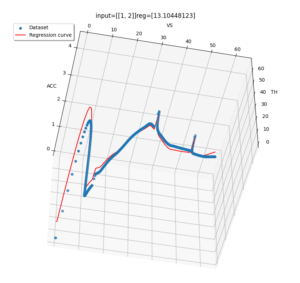
こんな感じのコードになりました。サポートベクタマシンのSVRを用いた回帰です。z = ax^2+ byという3次元的な放物線でこれを自動車に当てはめるとx:車速、y:加速度、z:アクセル開度といった感じになります。話元に戻って上述の3元1次式の回帰の結果です。簡略化のため簡単な放物線のみにしておきます。学習は-5<x<5、-10<y<10の範囲を上の図では0.02刻み、下の図では0.2刻みで学習、回帰の結果(赤線)です。カーネルはrbfです。
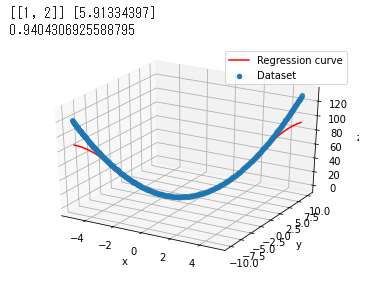
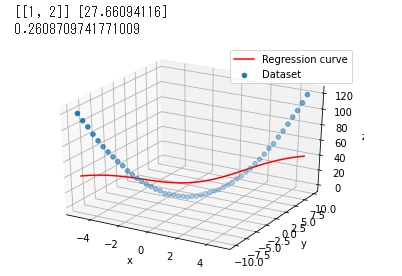
元の式にx=1,y=2を代入するとz=5*1^2+0.5*2=6が正解なのですが0.02刻みで学習した時は5.91、0.2の場合は27.66となり大きくずれています。
STEP3.python⇒Matlab
STEP.2で書いたpythonプログラムがMatlabで動くか試してみます。xyz.pyとファイル名を付けてMatlab上で実行するとこんな感じです。
pyrunfile("xyz.py")これで動きました。print文はコマンドウインド上に、plot画面はMatlabのfigureでなくpythonのfigureが起動して表示されます。意外と簡単です。あとはダイナミックシミュレーションはSimulinkで実行するのでMatlab環境で使いやすいようにpythonファイル内の変数をMatlabから引き渡し、pythonの実行結果をMatlabに戻すように工夫します。
import numpy as np
from sklearn import svm
import matplotlib.pyplot as plt
# データ
a = 5.0
b = 0.5
x = np.array(x) #MATLAB引数
y = np.array(y) #MATLAB引数
xy=np.vstack([x,y]) #SVM用データ
noise = np.random.normal(loc=0, scale=0.5, size=len(x))
z = a*x**2+ b*y +noise
z=z.tolist() #MATLABへの戻り値
# サポートベクターマシン
# 学習
model = svm.SVR(C=1.0, kernel='poly', degree=2,epsilon=0.1)
model.fit(xy.T, z)
# 予測
xy_sample = [[1,2]]
y_reg = model.predict(xy_sample)
print(xy_sample,y_reg) #予測結果参考(1点)
y_reg2 = model.predict(xy.T) #予測結果グラフ用
r2 = model.score(xy.T, z) # 決定係数算出
# グラフ(3D)
#fig = plt.figure()
fig, ax = plt.subplots(figsize=(6, 6), subplot_kw={'projection' : '3d'})
#ax=fig.add_subplot(1, 2, 1, projection='3d')
ax.scatter(x,y,z, label='Dataset', lw=1, marker="o")
ax.plot(x,y,y_reg2, label='Regression curve', color='red')
ax.legend(loc=2, shadow=True) # 凡例
ax.set_title('input='+str(xy_sample)+'reg='+str(y_reg)) # タイトル
plt.show()
plt.close()
先ほどのpythonプログラムの違いは
x = np.array(x) #MATLAB引数
y = np.array(y) #MATLAB引数
z=z.tolist() #MATLABへの戻り値
ファイル内のこの部分です。x,yを外部から与えzをnumpyのarrayで返すとMatlab上での処理が多少めんどくさそうなのでリスト形式で返すことにしました。matlab↔pythonで引数や戻り値の与え方については型などの条件あるようなので慣れないうちはこうした小さいプログラムで結果を評価しながら進めた方が良いかと思います。
で、Matlabでの実行結果はこんな感じになります。
x=[-5:0.5:5];
y=[-5:0.5:5];
z=pyrunfile("xyz2.py","z",x=x,y=y)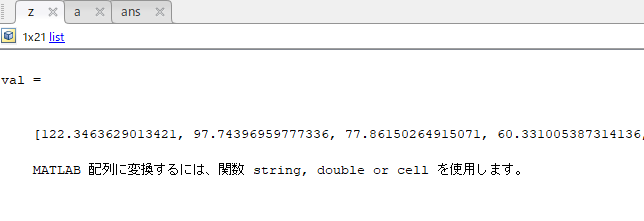
これでokです。戻り値zについてはリスト形式になる様なのであとでMatlab形式に変換したほうがいいのかもしれません。ちなみに
z=double(z)でOKです。
今回でpythonとMatlabをつなぐ方法が分かったと思います。次回は車両モデルの改修について説明したいと思います。モデルの改修は力学的な話しやプログラム上の問題点を考えながら進めるとかなり時間かかり趣旨から外れるので今回は最低限の改修にとどめたいと思います。ただ、サポートベクタマシンをSimulinkモデルに実装する都合上さらなる改修が必要になる場合は都度どうするか考えたいと思います。
尚本ページで示したSimulink車両はmathworks社作成の例題を抜粋しました。